🌨 云雪融

算法复习

🌏 Jan 01, 2025📖 12 min read

教学目标：掌握蛮力、分治、减治、变治和时空权衡等算法设计思想的特点

  • 蛮力：直接基于问题描述和涉及概念，常用于小规模例子，给出一个问题解的时间复杂度上界，衡量其它算法的时间效率，唯一一个能够应用于所有问题的策略。
  • 分治：划分大问题为多个小问题并解决合并。
  • 减治：大规模问题简化为一个小问题。
  • 变治：转换问题或数据结构。
  • 时空权衡：空间和时间的选择。

能够熟练使⽤蛮力法解决问题，作为优化的基线⽅法

找到最接近元素的差

int[] arr = {10, 8, 7, 5, 6, 1, 2, 3, 9, 4};
Arrays.sort(arr);
int minDiff = Integer.MAX_VALUE;
for (int i = 0; i < arr.length - 1; i++) {
    int diff = arr[i + 1] - arr[i];
    if (diff < minDiff) {
        minDiff = diff;
    }
}
System.out.println(minDiff);

找到凸包极点（顶点）

p2-p1 和 p3-p1 两个向量，夹角为锐角则叉积为正左侧，否则钝角为负右侧，直角为 0。

public static Set<Point> findConvexHull(List<Point> points) {
    Set<Point> hull = new HashSet<>();
    int n = points.size();
    for (int i = 0; i < n; i++) {
        for (int j = i + 1; j < n; j++) {
            Point p1 = points.get(i);
            Point p2 = points.get(j);
            boolean allOnOneSide = true;
            int side = 0;
            for (int k = 0; k < n; k++) {
                if (k == i || k == j) continue;
                Point p3 = points.get(k);
                double position = (p2.x - p1.x) * (p3.y - p1.y) - (p2.y - p1.y) * (p3.x - p1.x);
                if (position != 0) {
                    if (side == 0) {
                        side = (position > 0) ? 1 : -1;
                    } else if ((position > 0 && side == -1) || (position < 0 && side == 1)) {
                        allOnOneSide = false;
                        break;
                    }
                }
            }
            if (allOnOneSide) {
                hull.add(p1);
                hull.add(p2);
            }
        }
    }
    return hull;
}

分治思想在具体实现的时候，可以使⽤递归的⽅法，也可以结合特殊的数据结构使⽤循环的⽅法

合并排序根据位置分组，快速排序根据值分组。

合并排序

public static void mergeSort(int[] array) {
	if (array == null || array.length <= 1) return;
	int n = array.length;
	for (int step = 1; step < n; step *= 2) {
		for (int i = 0; i < n - step; i += 2 * step) {
			merge(array, i, i + step, Math.min(i + 2 * step, n));
		}
	}
}
private static void merge(int[] array, int low, int mid, int high) {
	int[] temp = new int[high - low];
	int i = low;
	int j = mid;
	int k = 0;
	while (i < mid && j < high) {
		if (array[i] <= array[j]) temp[k++] = array[i++];
		else temp[k++] = array[j++];
	}
	while (i < mid) temp[k++] = array[i++];
	while (j < high) temp[k++] = array[j++];
	System.arraycopy(temp, 0, array, low, temp.length);
}

快速排序

   public static void quickSort(int[] arr) {
        if (arr == null || arr.length <= 1) return;
        Stack<Integer> stack = new Stack<>();
        stack.push(0);
        stack.push(arr.length - 1);
        while (!stack.isEmpty()) {
            int end = stack.pop();
            int start = stack.pop();
            if (start < end) {
                int pivotIndex = partition(arr, start, end);
                stack.push(start);
                stack.push(pivotIndex - 1);
                stack.push(pivotIndex + 1);
                stack.push(end);
            }
        }
    }
    private static int partition(int[] arr, int start, int end) {
        int pivot = arr[end];
        int i = start - 1;
        for (int j = start; j < end; j++) {
            if (arr[j] < pivot) {
                i++;
                swap(arr, i, j);
            }
        }
        swap(arr, i + 1, end);
        return i + 1;
    }

能够采⽤分治思想解决的两个经典问题是最近对问题和凸包问题，请掌握具体的代码实现

最近对问题

    public static double distanceSquared(Point p1, Point p2) {
        return (p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y);
    }
    public static double closestPair(Point[] points) {
        Arrays.sort(points, Comparator.comparingDouble(p -> p.x));
        Arrays.sort(points, Comparator.comparingDouble(p -> p.y));
        return Math.sqrt(closestPairRecursive(points, 0, points.length - 1));
    }
 
    private static double closestPairRecursive(Point[] points, int l, int r) {
        int n = r - l + 1;
        if (n <= 3) {
            // 如果点的数量小于等于3，则直接计算最小距离
            double minDist = Double.POSITIVE_INFINITY;
            for (int i = l; i <= r; i++) {
                for (int j = i + 1; j <= r; j++) {
                    minDist = Math.min(minDist, distanceSquared(points[i], points[j]));
                }
            }
            return minDist;
        }
        // 分治步骤
        int mid = l + (r - l) / 2;
        Point midPoint = points[mid];
        double dl = closestPairRecursive(points, l, mid);
        double dr = closestPairRecursive(points, mid + 1, r);
        double d = Math.min(dl, dr);
        // 合并步骤，找出跨左右子集的最小距离
        Point[] strip = new Point[n];
        int j = 0;
        for (int i = l; i <= r; i++) {
            if (Math.abs(points[i].x - midPoint.x) < d) {
                strip[j++] = points[i];
            }
        }
        // 在strip中查找最小距离
        for (int i = 0; i < j; i++) {
            for (int k = i + 1; k < j && (strip[k].y - strip[i].y) < d; k++) {
                d = Math.min(d, distanceSquared(strip[i], strip[k]));
            }
        }
        return d;
    }

凸包问题

难点：合并两个凸包，先找到左凸包中最右的点和右凸包中最左的点，然后找上下共线点。

时空权衡思想在算法设计中应⽤非常⼴泛，例如字符串匹配、B 树，乃至动态规划

字符串匹配

Horspool

image.png

Boyer-Moore

image.png image.png

如果只用坏符号移动表或者好后缀移动表，BM 算法能够正确工作吗？为什么要一起使用？ 只用坏符号移动表和好后缀移动表都可以正确工作，只是效率降低。

B 树

贪心法

最小生成树

Prim：从点开始贪心选择。 Kruskal：从边开始贪心选择。 Dijkstra：不断更新未访问点的最短路径和。

活动相容

按照结束时间升序排列，依次选择靠前结束的，尽可能给后面留出更多时间余量执行更多活动。

public static int greedySelector(int [] s, int [] f, boolean a[]) {
	int n=s.length-1;
	a[1]=true;
	int j=1;
	int count=1;
	for (int i=2;i<=n;i++) {
		if (s[i]>=f[j]) {
			a[i]=true;
			j=i;
			count++;
		}
		else a[i]=false;
	}
	return count;
}

动态规划

最长公共子序列

 public int longestCommonSubsequence(String text1, String text2) {
	int n = text1.length();
	int m = text2.length();
	int[] pre = new int[m+1];// (i-1)层
	int[] cur = new int[m+1];// i 层
	for (int i = 1; i < n + 1; i++) {
		for (int j = 1; j < m + 1; j++) {
			if (text1.charAt(i-1) == text2.charAt(j-1))
				cur[j] = pre[j-1]+1;
			else cur[j] = Math.max(cur[j-1],pre[j]);
		}
		// 更新 (i-1) 层 为 i 层
		for (int j = 0; j < m + 1; j++) {
			pre[j] = cur[j];
		}
	}
	return cur[m];
}

最长回文子序列

public int longestPalindromeSubseq(String s) {
        int n = s.length();
        int[][] f = new int[n][n];
        for (int i = n - 1; i >= 0; i--) {
            f[i][i] = 1;
            for (int j = i + 1; j < n; j++) {
                if (s.charAt(i) == s.charAt(j)) {
                    f[i][j] = f[i + 1][j - 1] + 2;
                } else {
                    f[i][j] = Math.max(f[i + 1][j], f[i][j - 1]);
                }
            }
        }
        return f[0][n - 1];
    }

矩阵连乘

求多个矩阵连乘的最小次数。

public static void matrixChain(int [] p, int [][] m, int [][] s) {
	int n = p.length-1;
	for (int i = 1; i <= n; i++) m[i][i] = 0;
	for (int r = 2; r <= n; r++) {
		 for (int i = 1; i <= n - r + 1; i++) {
			int j = i + r - 1;
			m[i][j] = m[i+1][j] + p[i-1]*p[i]*p[j];
			s[i][j] = i;
			for (int k = i + 1; k < j; k++) {
			   int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
			   if (t < m[i][j]) {
				 m[i][j] = t;
				 s[i][j] = k;
				}
			}
		}
	}
}

了解平滑函数性质，能⽤主定理求解递归⽅程，判断当前⽅程适⽤主定理哪⼀类型，进而解出递归式

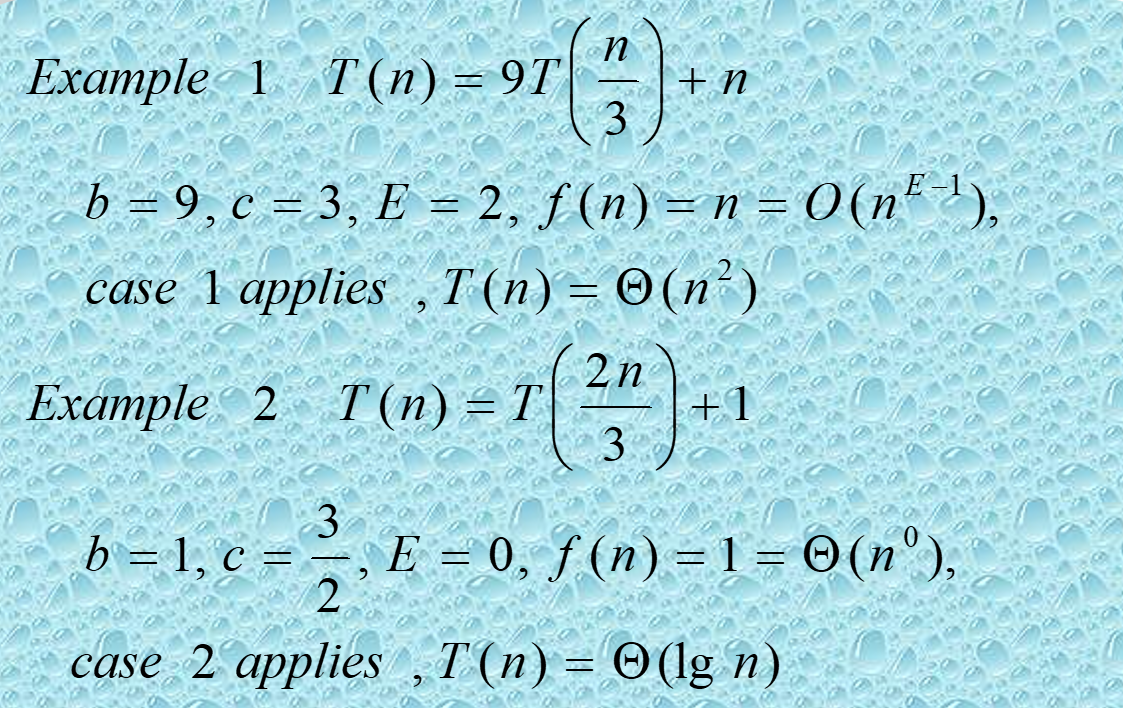
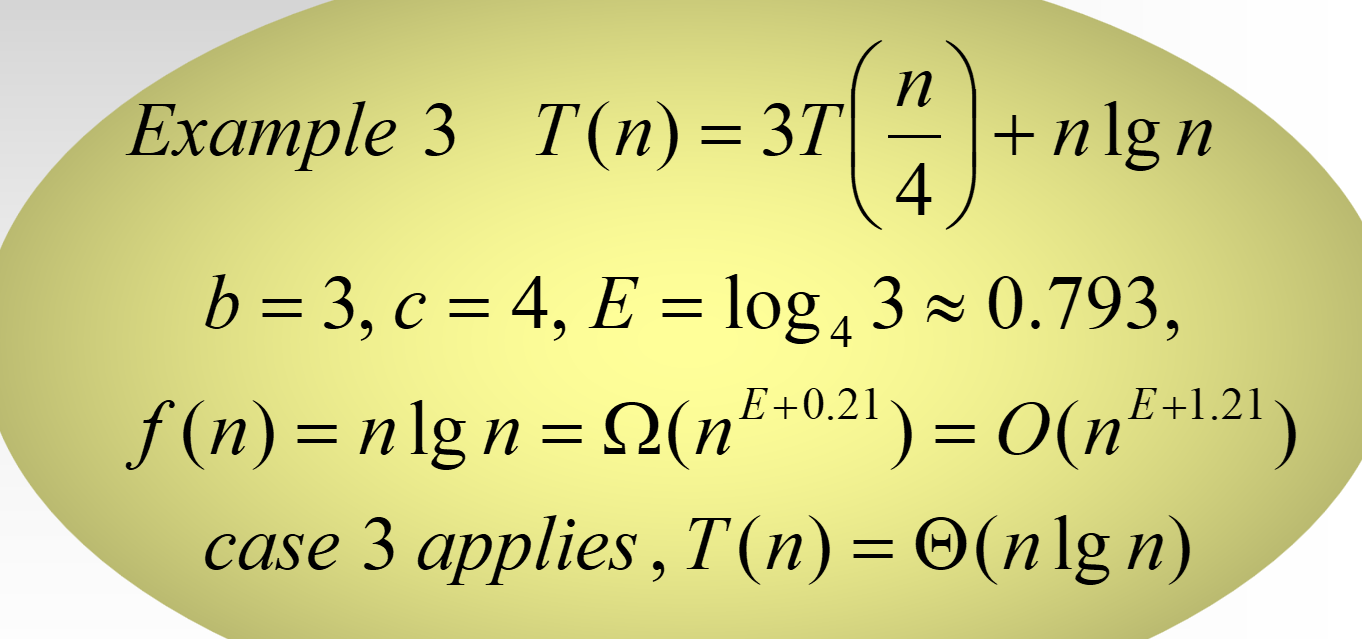
image.png image.png image.png

不符合三种情形中的任意一种，因此： image.png

复杂度的表示法：O(f)、(f)和 Θ(f)的含义，基于三种表示的⼀系列性质

对于两个函数 和 ，如果存在正数 和正整数 ， 使得对于所有，都有， 那么 。 对于两个函数 和 ，如果存在正数 和正整数 ， 使得对于所有，都有， 那么 。 对于两个函数 和 ，如果存在正数 、 和正整数 ， 使得对于所有，都有， 那么 。 image.png

介绍 NPC 理论的含义和实际应⽤价值，能列举 NPC 问题，证明⼀些主要的 NPC 问题（如装箱问题，0-1 背包）既是 NP 的也是 NP-hard 的

首先证明 NP，然后证明 NPH。 image.png 装箱问题： image.png

近似算法的定义，如何衡量近似算法的好坏，能掌握对于装箱问题的几种贪⼼算法（First Fit Algorithm - FF，Next Fit Algorithm - NF，First Fit Decreasing - FFD）。 在线算法的定义，以上哪个算法是在线算法，复杂度如何

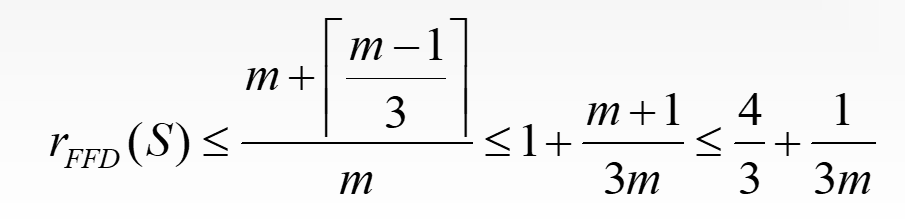
FFD，不是在线算法，FF 和 NF 是在线算法。 image.png image.png

在线分箱的定义：

  • 条目是一个接一个输入的，这意味着算法在输入结束前永远不知道输入何时结束。
  • 对于装箱，每个条目都必须先放入一个箱，然后才能处理下一个条目。
  • 由于输入可能在任何时候结束，因此，任何最优解在任何时候都应该是已处理输入的最优解。 在最坏的情况下，任何在线分箱打包算法都至少使用最佳分箱数的 4/3。证明：先 n 个（1/2-），然后 n 个（1/2+）。

image.png 需要注意的是，没有两个连续的分仓可以包含总值小于 1 的对象，这意味着最多浪费一半的空间。 存在 NF 使用 2m-2 bins 的输入。 举个例子输入序列 S 由 n 个项目组成（对于某个整数 k，n=4k）。奇数 i 的 si 大小为 0.5，偶数 i 的 si 大小为 2/n。 最佳的分仓数为 n/4+1（n/4 表示 2 个大小均为 0.5 的分仓，1 表示所有大小为 2/n 的分仓）。 NF 使用 n/2 个分仓。 NF 复杂度。 image.png

🔀随便看看